内容は下記の通り。
- 3 章 - ベルヌーイ分布に従う確率変数 X におけるパラメータ $\theta$ の事後分布と予測分布
- 8 章 - 藤井七段(棋士)の勝率についての実データを用いた分析
以下では確率変数 X およびベルヌーイ分布のパラメータ $\theta$ が下記に従うものとして話を進める。
\begin{eqnarray} \label{bernoulli} X &\sim& Bernoulli(\theta) \\ \label{beta} \theta &\sim& Beta(a, b) \end{eqnarray}
1 理論の話
紙とペンで計算を行う事により各種概念を定義および導出していく。
1.1 事後分布
事後分布 $p(\theta | x^{n} )$ についてまずベイズの公式により下記が成立する。 \begin{eqnarray} p(\theta | x^{n}) &=& \frac{ p(x^{n} | \theta) \varphi(\theta) }{ \int p(x^{n} | \theta) \varphi(\theta) d\theta } \nonumber \end{eqnarray} ここで \[ Z_{n} \stackrel{\mathrm{def}}{=} \int_{0}^{1} p(x^{n} | \theta) \varphi(\theta) d\theta \] とおくと \begin{eqnarray} p(\theta | x^{n}) &=& \frac{ p(x^{n} | \theta) \varphi(\theta) }{ Z_{n} } \nonumber \\ &=& \frac{ 1 }{ Z_{n} } \prod_{j = 1}^{n} p(x_{j} | \theta) \cdot \varphi(\theta) ~~~ (\because (\ref{bernoulli}) および X は独立試行) \nonumber \end{eqnarray} となり、このとき ($\ref{bernoulli}$) ($\ref{beta}$) により \begin{eqnarray} p(x | \theta) &=& \theta^{x} (1 - \theta)^{1 - x} & ~~~ \because (\ref{bernoulli}) \nonumber \\ \varphi(\theta) &=& \frac{ 1 }{ B(a, b) } \theta^{ a - 1 } (1 - \theta)^{ b - 1 } & ~~~ \because (\ref{beta}) \nonumber \end{eqnarray} となる事から \begin{eqnarray} p(\theta | x^{n} ) &=& \frac{ 1 }{ Z_{n} } \prod_{j} \theta^{ x_{j} } (1 - \theta)^{ 1 - x_{j} } \cdot \frac{ \theta^{ a - 1 } (1 - \theta)^{ b - 1 } }{ B(a, b) } \nonumber \\ &=& \frac{ 1 }{ Z_{n} } \theta^{ \sum x_{j} } (1 - \theta)^{ n - \sum x_{j} } \cdot \frac{ \theta^{ a - 1 } (1 - \theta)^{ b - 1 } }{ B(a, b) } \nonumber \\ &=& \frac{ 1 }{ Z_{n} \cdot B(a, b) } \theta^{ a + \sum x_{j} - 1 } \cdot (1 - \theta)^{ n + b - \sum x_{j} - 1 } \nonumber \\ \end{eqnarray} が成立する。
ここで $p(\theta | x^{n})$ が確率分布 ($\therefore \int_{0}^{1} p(\theta | x^{n}) d\theta = 1 $) であり $ Z_{n} \cdot B(a, b) $ がその規格化定数である事から \begin{eqnarray} Z_{n} \cdot B(a, b) &=& \int_{0}^{1} \theta^{ a + \sum x_{j} - 1 } (1 - \theta)^{ n + b - \sum x_{j} - 1 } d\theta \nonumber \\ \nonumber \\ &=& B(a + \sum_{j=1}^{n} x_{j}, n + b - \sum_{j=1}^{n} x_{j}) ~~~ (\because ベータ関数の定義) \nonumber \end{eqnarray} となり、よって \begin{eqnarray} p(\theta | x^{n}) &=& \frac{ \theta^{ a + \sum x_{j} - 1} (1 - \theta)^{ n + b - \sum x_{j} - 1 } }{ B(a + \sum x_{j}, n + b - \sum x_{j}) } \nonumber \\ \nonumber \\ &=& Beta(\theta | a + \sum_{j=1}^{n} x_{j}, n + b - \sum_{j=1}^{n} x_{j}). ~~~ (\because ベータ分布の定義) \nonumber \end{eqnarray}
\begin{eqnarray} \label{post_theta} \therefore p(\theta | x^{n}) = Beta(\theta | a + \sum_{j=1}^{n} x_{j}, n + b - \sum_{j=1}^{n} x_{j}). \end{eqnarray}
1.1.1 MAP
($\ref{post_theta}$) より事後分布 $p(\theta | x^{n})$ がベータ分布に従う事から以下ではベータ分布の極値を求める事により事後分布 $p(\theta | x^{n})$ の点推定値の 1 つである MAP(Maximum A Posteriori: 最大事後確率) を導出する。
\begin{eqnarray} \frac{d}{d\theta} Beta(\theta | \alpha, \beta) &=& \frac{d}{d\theta} \frac{1}{B(\alpha, \beta)} \theta^{\alpha-1} \cdot (1-\theta)^{\beta-2} \nonumber \\ &=& \frac{1}{B(\alpha, \beta)} \{ (\alpha-1) \theta^{\alpha-2} \cdot (1 - \theta)^{\beta-1} + \theta^{\alpha-1} \cdot (\beta-1)(1-\theta)^{\beta-2} (-1) \} \nonumber \\ &=& \frac{1}{B(\alpha, \beta)} \theta^{\alpha-2} \cdot (1-\theta)^{\beta-2} \{ (\alpha-1) \cdot (1-\theta) - \theta \cdot (\beta-1) \} \nonumber \\ &=& \frac{1}{B(\alpha, \beta)} \theta^{\alpha-2} \cdot (1-\theta)^{\beta-2} \{ (\alpha-1) - (\alpha + \beta - 2) \theta \} \nonumber \end{eqnarray} により \begin{eqnarray} \frac{d}{d\theta} Beta(\theta | \alpha, \beta) = 0 \nonumber \\ \Leftrightarrow \theta = \frac{\alpha-1}{\alpha+\beta-2} . \nonumber \end{eqnarray} 上記の成立および事後分布 ($\ref{post_theta}$) で $\alpha = a + \sum x_{j}, \beta = n + b - \sum x_{j}$ と読み替える事により \begin{eqnarray} \label{MAP} \therefore \hat{\theta}_{MAP} = \frac{a + \sum x_{j} - 1}{n + a + b - 2}. \end{eqnarray}
1.1.2 MLE
ここでは上記で考えた事後分布とは別に ($\ref{bernoulli}$) に従って尤度関数 $L(\theta)$ を考える事により MLE(Maximum Likelihood Estimator: 最尤推定量) の実現値 $\hat{\theta}_{MLE}$ を導出する。 \begin{eqnarray} L(\theta) &=& p(x^{n} | \theta) \nonumber \\ &=& \prod_{j=1}^{n} \theta^{x_{j}} (1 - \theta)^{1 - x_{j}} \nonumber \\ &=& \theta^{\sum x_{j}} \cdot (1 - \theta)^{n - \sum x_{j}} \nonumber \end{eqnarray} により対数尤度関数 $log L(\theta)$ を $\theta$ で微分して下記を得る。 \begin{eqnarray} \frac{d}{d\theta} log L(\theta) &=& \frac{d}{d\theta} \{ (\sum_{j=1}^{n} x_{j}) \cdot log \theta + (n - \sum_{j=1}^{n} x_{j}) \cdot log(1 - \theta) \} \nonumber \\ &=& \frac{\sum x_{j}}{\theta} - \frac{n - \sum x_{j}}{1 - \theta}. \nonumber \end{eqnarray} よって \begin{eqnarray} &&\frac{d}{d\theta} log L(\theta) = 0 \nonumber \\ \nonumber \\ &\Leftrightarrow& \frac{\sum x_{j}}{\theta} = \frac{n - \sum x_{j}}{1 - \theta} \nonumber \\ &\Leftrightarrow& \theta = \frac{1}{n} \sum_{j=1}^{n} x_{j}. \nonumber \end{eqnarray} \begin{eqnarray} \label{MLE} \therefore \hat{\theta}_{MLE} = \frac{1}{n} \sum_{j=1}^{n} x_{j}. \end{eqnarray}
1.1.3 無情報事前分布における MAP と MLE の一致
MAP ($\ref{MAP}$) における事前分布として無情報事前分布を適用する事を考える。
具体的には ($\ref{beta}$) における $a = b = 1$ の適用であり、$Beta(\theta | 1, 1)$ は定義域 $[0, 1]$ における一様分布である。
このとき下記が成立し、無情報事前分布における MAP($\ref{MAP}$) と MLE($\ref{MLE}$) の一致というよく知られた結果が導出される。 \begin{eqnarray} \hat{\theta}_{MAP} &=& \frac{1 + \sum x_{j} - 1}{n + 1 + 1 - 2} \nonumber \\ &=& \frac{1}{n} \sum_{j=1}^{n} x_{j} \nonumber \\ &=& \hat{\theta}_{MLE}. \nonumber \end{eqnarray}
1.2 予測分布
事後分布 $p(\theta | x^{n})$ による確率モデル $p(x|\theta)$ の期待値を予測分布(predictive distribution) $p^{\ast}(x)$ と定義する。 \begin{eqnarray} p^{*}(x) \stackrel{\mathrm{def}}{=} E_{ p(\theta | x^{n}) }[ p(x | \theta)]. \nonumber \end{eqnarray} ここで ($\ref{bernoulli}$) および事後分布 ($\ref{post_theta}$) により予測分布 $p^{\ast}(x)$ は下記で表される。 \begin{eqnarray} p^{\ast}(x) &=& E_{ p(\theta | x^{n}) }[ p(x | \theta)] \nonumber \\ &=& \int_{0}^{1} p(x | \theta) \cdot p(\theta | x^{n}) d\theta \nonumber \\ &=& \int_{0}^{1} Bernoulli(x | \theta) \cdot Beta(a + \sum x_{j}, b + b - \sum x_{j}) d\theta \nonumber \\ &=& \int_{0}^{1} \theta^{x} (1 - \theta)^{ 1 - x } \cdot \frac{ \theta^{ \alpha - 1 } (1 - \theta)^{ \beta - 1 } }{ B(\alpha, \beta) } d\theta \nonumber \\ \label{pred_dist} &=& \frac{ B(\alpha + x, \beta - x + 1) }{ B(\alpha, \beta) }. \end{eqnarray} ただし上記において $\alpha \stackrel{\mathrm{def}}{=} a + \sum x_{j}, \beta \stackrel{\mathrm{def}}{=} n + b - \sum x_{j}$ により $\alpha$ と $\beta$ を定義するものとする。
1.2.1 EAP
予測分布 ($\ref{pred_dist}$) において特に $x=1$ とおくと \begin{eqnarray} p^{*}(x=1) &=& \int_{0}^{1} \theta \cdot \frac{ \theta^{ \alpha - 1 } (1 - \theta)^{ \beta - 1 } }{ B(\alpha, \beta) } d\theta \nonumber \\ &=& \int_{0}^{1} \theta \cdot p(\theta | x^{n}) d\theta \nonumber \\ &=& E_{ p(\theta | x^{n}) }[\theta]. \nonumber \end{eqnarray}
ここで事後分布 $p(\theta | x^{n})$ における $\theta$ の期待値(平均) $E_{ p(\theta | x^{n}) }[\theta]$ を EAP(Expectd A Posterior estimate) 推定値と呼び、下記が成立する。 \begin{eqnarray} \hat{\theta}_{EAP} &\stackrel{\mathrm{def}}{=}& E_{ p(\theta | x^{n}) }[\theta] \nonumber \\ &=& p^{*}(x=1) \nonumber \\ \label{EAP_incomplete} &=& \frac{ B(\alpha + 1, \beta) }{ B(\alpha, \beta) }. \end{eqnarray} ここでベータ関数の性質より \begin{eqnarray} B(\alpha + 1, \beta) &=& \int_{0}^{1} x^{ \alpha } (1 - x)^{ \beta - 1 } dx \nonumber \\ &=& [ x^{\alpha} \cdot \frac{1}{\beta} (1 - x)^{\beta} (-1) ]_{0}^{1} + \frac{\alpha}{\beta} \int_{0}^{1} x^{\alpha-1} (1 - x)^{\beta} dx \nonumber \\ &=& \frac{\alpha}{\beta} \int_{0}^{1} x^{\alpha-1} (1-x)^{\beta-1} (1-x)^{1} dx \nonumber \\ &=& \frac{\alpha}{\beta} ( \int_{0}^{1} x^{\alpha-1} (1-x)^{\beta-1} dx - \int_{0}^{1} x^{\alpha}(1-x)^{\beta-1} dx ) \nonumber \\ &=& \frac{\alpha}{\beta} ( B(\alpha, \beta) - B(\alpha + 1, \beta) ). \nonumber \end{eqnarray} 右辺の $B(\alpha + 1, \beta)$ を移項して \begin{eqnarray} (1 + \frac{\alpha}{\beta}) B(\alpha + 1, \beta) = \frac{\alpha}{\beta} B(\alpha, \beta). \nonumber \end{eqnarray} よって \begin{eqnarray} \label{beta_them} \therefore B(\alpha + 1, \beta) = \frac{\alpha}{\alpha + \beta} B(\alpha, \beta). \end{eqnarray} 上記 ($\ref{beta_them}$) を ($\ref{EAP_incomplete}$) に適用する事で下記を得る。 \begin{eqnarray} \hat{\theta}_{EAP} &=& \frac{ B(\alpha + 1, \beta) }{ B(\alpha, \beta) } \nonumber \\ &=& \frac{1}{B(\alpha, \beta)} \cdot \frac{\alpha}{\alpha + \beta} B(\alpha, \beta) \nonumber \\ &=& \frac{ \alpha }{ \alpha + \beta } \nonumber \\ &=& \frac{ a + \sum x_{j} }{ a + b + n }. \nonumber \end{eqnarray}
\begin{eqnarray} \label{EAP} \therefore \hat{\theta}_{EAP} = \frac{ a + \sum x_{j} }{ a + b + n }. \end{eqnarray}
1.3 まとめ
\begin{eqnarray} X &\sim& Bernoulli(\theta) \nonumber \\ \theta &\sim& Beta(a, b) \nonumber \end{eqnarray} の下で下記が成立。 \begin{eqnarray} p(\theta | x^{n}) &=& Beta(a + \sum_{j=1}^{n} x_{j}, n + b - \sum_{j=1}^{n} x_{j}) \nonumber \\ \hat{\theta}_{MAP} &=& \frac{a + \sum x_{j} - 1}{n + a + b - 2} \nonumber \\ \hat{\theta}_{EAP} &=& \frac{ a + \sum x_{j} }{ a + b + n } \nonumber \\ \hat{\theta}_{MLE} &=& \frac{1}{n} \sum_{j=1}^{n} x_{j} \nonumber \\ p^{\ast}(x) &=& E_{ p(\theta | x^{n}) }[ p(x | \theta)] \nonumber \end{eqnarray}
2 実データで試す
8 章に記載されている将棋の藤井七段の戦績データを用いて勝率を推定していく。
2.1 データ
生データ及びこの後に記載する R のコードは
fujii_game_results@github
を参照
※スクレイピング用のコードも上記にあり
| date | first_or_second | result |
|---|---|---|
| 2016-12-24 | 後 | ○ |
| 2017-01-26 | 先 | ○ |
| 2017-02-09 | 後 | ○ |
2.2 勝率の推定
事前分布として Beta 分布を仮定し、($\ref{MAP}$) ($\ref{MLE}$) ($\ref{EAP}$) により各種推定値の推移を可視化する。
2.2.1 事前分布
事前分布として $Beta(\theta | 2, 2)$ を仮定する。
library(tidyverse)
# 事前分布
a <- 2
b <- 2
tibble(theta = seq(0, 1, 0.01), density = dbeta(theta, a, b)) %>%
ggplot(aes(theta, density)) +
geom_line()
2.2.2 分析データの生成
事前に算出した MAP/EAP/MLE により勝率を推定したデータを作成。
df.results <- readr::read_csv(
file = "https://raw.githubusercontent.com/you1025/fujii_game_results/master/data/fujii.csv",
col_types = cols(
date = col_date(format = ""),
first_or_second = col_character(),
result = col_character()
)
) %>%
dplyr::mutate(
# 対戦番号の付与
game = dplyr::row_number(),
# 先攻フラグ
flg_first = (first_or_second == "先"),
# 勝利フラグ
flg_win = (result == "○"),
# 通算勝利数
cumsum_win = cumsum(flg_win),
# 推定値
MLE = cumsum_win / game,
EAP = (a + cumsum_win) / (a + b + game),
MAP = (a + cumsum_win - 1) / (a + b + game - 2)
) %>%
# 対戦前のレコードを追加
dplyr::bind_rows(tibble(game = 0, cumsum_win = 0, EAP = a / (a + b))) %>%
dplyr::arrange(game) %>%
# 事後分布の 2.5%, 97.5% タイルを算出
dplyr::mutate(
q.025 = qbeta(p = 0.025, shape1 = a + cumsum_win, shape2 = b + game - cumsum_win),
q.975 = qbeta(p = 0.975, shape1 = a + cumsum_win, shape2 = b + game - cumsum_win)
) %>%
dplyr::select(
game,
flg_first,
flg_win,
cumsum_win,
MLE,
EAP,
MAP,
q.025,
q.975
)
| game | flg_first | flg_win | cumsum_win | MLE | EAP | MAP | q.025 | q.975 |
|---|---|---|---|---|---|---|---|---|
| 0 | NA | NA | 0 | NA | 0.500 | NA | 0.094 | 0.905 |
| 1 | F | T | 1 | 1.000 | 0.600 | 0.666 | 0.194 | 0.932 |
| 2 | T | T | 2 | 1.000 | 0.666 | 0.750 | 0.283 | 0.947 |
2.2.3 勝率の推移
# 勝率の推移
df.results %>%
ggplot(aes(game)) +
geom_line(aes(y = MLE), linetype = 2, alpha = 1/2) +
geom_line(aes(y = EAP), linetype = 1, colour = "tomato") +
geom_line(aes(y = MAP), linetype = 1, colour = "blue", alpha = 1/3) +
geom_ribbon(aes(ymin = q.025, ymax = q.975), alpha = 1/7) +
scale_y_continuous(limits = c(0, 1), labels = scales::percent) +
labs(
x = "Games",
y = NULL
)
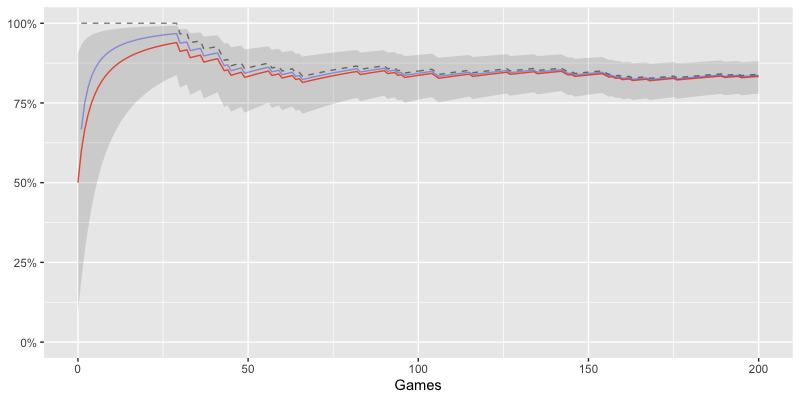
- 対戦数の少ない段階では MLE(黒色点線) の勝率が 100% と過度にデータを反映した値になってしまっている事がわかる
- EAP(赤色) が最も低い値となっており MAP(青色) が EAP と MLE の間に挟まれるような値となっている
- 対戦が進むにつれ 2.5%〜97.5% タイルの幅が狭くなり確信が高まっていく様子が見て取れる
2.2.4 事後分布の変遷
# 対戦ごとの事後分布の一覧
df.results %>%
dplyr::mutate(
# 対戦が進む度に事後分布を推定する
data = map2(game, cumsum_win, function(game, cumsum_win) {
tibble(
x = seq(0, 1, 0.001),
d = dbeta(x, shape1 = a + cumsum_win, b + game - cumsum_win)
)
})
) %>%
tidyr::unnest(data) %>%
ggplot(aes(x, d)) +
geom_line(aes(group = game, colour = game), alpha = 1/3) +
scale_colour_gradient(low = "blue", high = "tomato") +
labs(
x = "勝率",
y = NULL
) +
scale_x_continuous(labels = scales::percent) +
theme_gray(base_family = "Osaka")
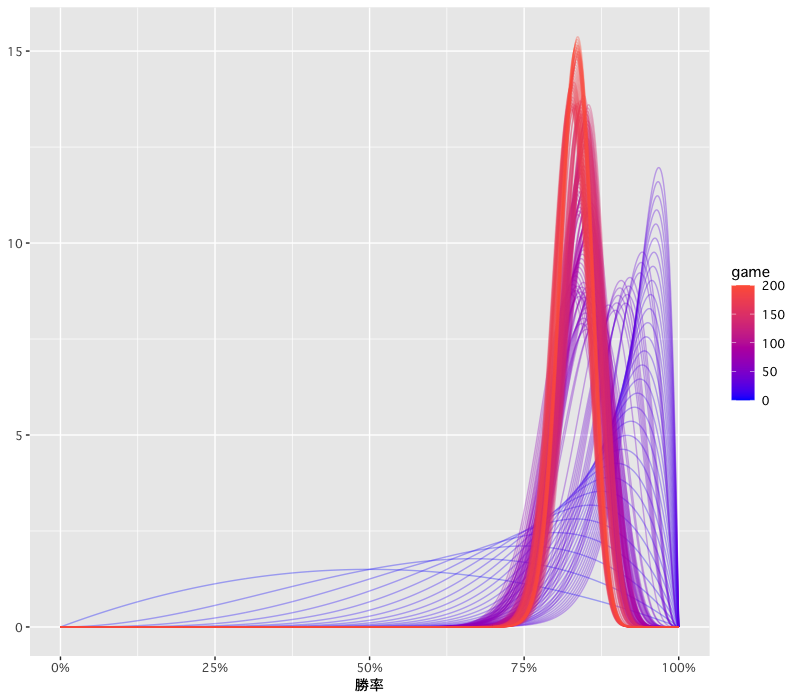
- 対戦が進む(赤色が強くなる)ごとに 80% 付近にピークが集まり、高さが増していく事から確信が高まっている様子が見て取れる
参考