- どの程度の差異が発生するのか
- どのように差異が収斂していくのか
この記事は以前に記載した ベルヌーイ分布と事後分布 の 「1.1.3 無情報事前分布における MAP と MLE の一致」 で簡潔に述べた内容を含み、より広い条件で検証するものである。
1. 導出された結果(再掲)
以前の記事で導出した結果のみを下記に記載する。
※詳細な定義および導出の過程は ベルヌーイ分布と事後分布 を参照
- $p(\theta | x^{n})$: 事後分布
- $x_{j}$: サンプルデータ
- $n$: サンプル数
- $a, b$: 事前分布 $Beta(a,b)$ のパラメータ
\begin{eqnarray} p(\theta | x^{n}) &=& Beta(a + \sum_{j=1}^{n} x_{j}, n + b - \sum_{j=1}^{n} x_{j}) \\ \hat{\theta}_{MLE} &=& \frac{1}{n} \sum_{j=1}^{n} x_{j} \\ \hat{\theta}_{MAP} &=& \frac{a + \sum x_{j} - 1}{n + a + b - 2} \\ \hat{\theta}_{EAP} &=& \frac{ a + \sum x_{j} }{ n + a + b } \end{eqnarray}
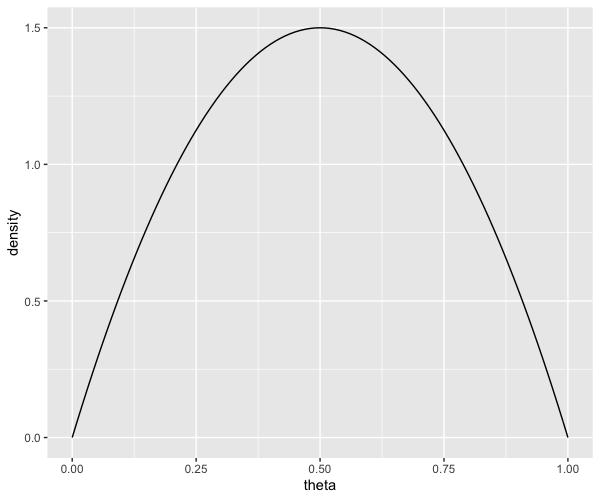
2. 事前分布
上記ではベルヌーイ施行における事前分布としてベータ分布を仮定しており、以下ではパラメータ $a, b$ を 2 パターン設定して検証を行う。
- (a, b) = (1, 1)
- (a, b) = (3, 6)
library(tidyverse)
# Beta 分布のパラメータ
lst.beta <- list(
a = 3,
b = 6
)
tibble(
p = seq(0, 1, 0.01),
d_1_1 = dbeta(0, 1, 1), # Beta(1,1)
d_a_b = dbeta(p, lst.beta$a, lst.beta$b) # Beta(a,b)
) %>%
# to wide-form
tidyr::pivot_longer(cols = -p, names_to = "param", values_to = "density") %>%
# 可視化
ggplot(aes(p, density)) +
geom_line() +
labs(y = NULL) +
facet_grid(
. ~ param,
labeller = labeller(
param = as_labeller(c(
"d_1_1" = "B(1,1)",
"d_a_b" = stringr::str_c("Beta(", lst.beta$a, ",", lst.beta$b, ")")
))
)
)
2. データの生成
真のパラメータ $p = 0.3$ を指定して 1,000 個の TRUE/FALSE からなる乱数 $x$ を生成する。
set.seed(1025) n <- 1000 p <- 0.3 # データ生成 x <- rbernoulli(n, p) # 先頭 10 件の確認 x[1:10] # FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE FALSE FALSE # x の平均値 # 真のパラメータ p=0.3 にかなり近い mean(x) # 0.29
上記 $x$ を用いて各累積施行ごとにパラメータ $p$ を推定していく。
※コメント内の番号 (1)〜(4) は 「1. 導出された結果(再掲)」 における数式の番号に紐づく
df.estimations <- tibble(
# 延べ試行回数
n = 1:length(x),
# 成功: 1
# 失敗: 0
x = as.integer(x),
# 延べ成功回数
cumsum_x = cumsum(x),
# 最尤推定による点推定値 - (2)
MLE = cumsum_x / n,
# MAP - (3)
MAP_1_1 = (1 + cumsum_x - 1) / (n + 1 + 1 -2), # 事前分布: Beta(1,1)
MAP_a_b = (lst.beta$a + cumsum_x - 1) / (n + lst.beta$a + lst.beta$b -2), # 事前分布: Beta(3,6)
# EAP - (4)
EAP_1_1 = (1 + cumsum_x) / (1 + 1 + n), # 事前分布: Beta(1,1)
EAP_a_b = (lst.beta$a + cumsum_x) / (lst.beta$a + lst.beta$b + n), # 事前分布: Beta(3,6)
# 事後分布の算出 - (1)
post_dists = purrr::map2(n, cumsum_x, function(n, cumsum_x, a, b) {
tibble::tibble(
p = seq(0, 1, 0.01),
post_d_1_1 = dbeta(p, 1 + cumsum_x, n + 1 - cumsum_x), # 事前分布: Beta(1,1)
post_d_a_b = dbeta(p, a + cumsum_x, n + b - cumsum_x) # 事前分布: Beta(3,6)
)
}, a = lst.beta$a, b = lst.beta$b)
)
| n | x | cumsum_x | MLE | MAP_1_1 | MAP_a_b | EAP_1_1 | EAP_a_b | post_dists |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0.25 | 0.333 | 0.3 | <tibble [101 × 3]> |
| 2 | 0 | 0 | 0 | 0 | 0.222 | 0.25 | 0.273 | <tibble [101 × 3]> |
| 3 | 0 | 0 | 0 | 0 | 0.2 | 0.2 | 0.25 | <tibble [101 × 3]> |
| 4 | 0 | 0 | 0 | 0 | 0.182 | 0.167 | 0.231 | <tibble [101 × 3]> |
| 5 | 0 | 0 | 0 | 0 | 0.167 | 0.143 | 0.214 | <tibble [101 × 3]> |
上記 post_dists 項目には各行(累積施行)ごとに事後分布のデータが tibble 形式で格納されており、項目を指定しないと確認する事はできない。
下記は 1 回目の施行によりデータを 1 つ獲得した後の事後分布を 5 行だけ表示したものであり、post_d_xxx は確率密度を表す。
| p | post_d_1_1 | post_d_a_b |
|---|---|---|
| 0 | 2 | 0 |
| 0.01 | 1.98 | 0.0237 |
| 0.02 | 1.96 | 0.0893 |
| 0.03 | 1.94 | 0.189 |
| 0.04 | 1.92 | 0.316 |
3. 事後分布の確認
各施行ごとの事後分布を確認していく。
3.1 少ない試行回数での挙動
試行回数が少ない時の挙動を確認する。主に 1〜10 回をメインに観察する。
df.estimations%>%
# 試行回数が特定の時点のみを対象
dplyr::filter(n %in% c(1, 2, 3, 4, 5, 10, 25, 50, 100)) %>%
# 事後分布の抽出
tidyr::unnest(post_dists) %>%
dplyr::select(n, MLE, p, post_d_1_1, post_d_a_b) %>%
# => long-form
tidyr::pivot_longer(cols = c(post_d_1_1, post_d_a_b), names_to = "type", values_to = "density") %>%
# 可視化
ggplot(aes(p, density)) +
geom_line(aes(colour = type), alpha = 1, show.legend = F) +
geom_vline(aes(xintercept = MLE), size = 1.0, linetype = "solid", colour = "gray") +
labs(
x = NULL,
y = NULL
) +
facet_grid(
n ~ type,
scale = "free_y",
labeller = labeller(
type = as_labeller(c(
"post_d_1_1" = "Beta(1,1)",
"post_d_a_b" = stringr::str_c("Beta(", lst.beta$a, ",", lst.beta$b, ")")
))
)
)
左列には $Beta(1,1)$ を事前分布(無情報事前分布)とする事後分布が、右列には $Beta(3,6)$ を事前分布とする事後分布が表示されている。
右側の番号は試行回数を表しており、下に進むほど試行回数が大きくなる。
各セルにおける横軸上の三角は MLE を表しており、各行ごとに左右の列で同じ位置に表示されている事に注意。
上記より把握できる事を下記にまとめる。
- 試行回数が少ない場合に MLE はデータに過度に反応し、試行回数 1〜5 では p = 0 という極端な値を提示してしまっている
- 左列である Beta(1,1) (無情報事前分布)側におけるピークの位置(MAP) と MLE は一致している(理論上完全に一致する)
- 最初の 5 回で FALSE が続いている事を受けて Beta(1,1) 側はデータに過度に反応した事後分布を生成してしまっている
- 最初の 5 回の FALSE で Beta(1,1) 側は試行回数が増える程に p = 0 の確信が高まっている様子が伺える
- 試行回数が少ない時点では Beta(1,1) 側と Beta(3,6) 側では差異が大きい
- 試行回数が大きくなるにつれ Beta(1,1) 側と Beta(3,6) 側の差異は縮まる傾向にある
- Beta(1,1) 側および Beta(3,6) 側の両方で、試行回数が増えるにつれてピーク付近でのばらつきが減少している(横が狭くなる)事およびピークの位置が高くなっている事から段々と推定の確信が高まっている様子が伺える
3.2 事前分布による差異
$Beta(1,1)$ と $Beta(3,6)$ の異なる事前分布における挙動の差異を確認する。
df.estimations %>%
dplyr::select(n, MAP_1_1, MAP_a_b, EAP_1_1, EAP_a_b) %>%
# => long-form
tidyr::pivot_longer(cols = c(MAP_1_1, MAP_a_b, EAP_1_1, EAP_a_b), names_pattern = "(MAP|EAP)_(.+_.+)", names_to = c("type", "param"), values_to = "prob") %>%
# 可視化
ggplot(aes(n, prob)) +
geom_line(aes(color = param), alpha = 1/2) +
geom_point(aes(colour = param), size = 0.75, alpha = 1/5) +
# 真のパラメータ 0.3 を表示
geom_hline(yintercept = 0.3, alpha = 1/3) +
scale_y_continuous(limits = c(0, 0.5)) +
scale_colour_hue(
name = "Prior Dist",
labels = c(
"1_1" = "Beta(1,1)",
"a_b" = stringr::str_c("Beta(", lst.beta$a, ",", lst.beta$b, ")")
)
) +
labs(
x = "Trials",
y = "Estimated Parameter"
) +
facet_grid(type ~ .)
横軸に試行回数、縦軸にパラメータ p の推定値を表示する。
水平に伸びた直線はパラメータ p の真の値 0.3 を示している。
上下で推定値が異なる事に注意。
- Beta(1,1) (無情報事前分布)を用いた推定値の方が上下の振れ幅が大きい傾向にある
- MAP/EAP ともに試行回数が少ない範囲では事前分布の違いにより挙動が大きく異る
- 試行回数が大きくなると事前分布による差異はほぼ見られくなる
3.3 点推定値による差異
MAP と EAP における挙動の差異を確認する。
df.estimations %>%
dplyr::select(n, MAP_1_1, MAP_a_b, EAP_1_1, EAP_a_b) %>%
# => long-form
tidyr::pivot_longer(cols = c(MAP_1_1, MAP_a_b, EAP_1_1, EAP_a_b), names_pattern = "(MAP|EAP)_(.+_.+)", names_to = c("type", "param"), values_to = "prob") %>%
# 可視化
ggplot(aes(n, prob)) +
geom_line(aes(color = type), alpha = 1/2) +
geom_point(aes(colour = type), size = 0.75, alpha = 1/5) +
# 真のパラメータ 0.3 を表示
geom_hline(yintercept = 0.3, alpha = 1/3) +
scale_y_continuous(limits = c(0, 0.5)) +
labs(
colour = NULL,
x = "Trials",
y = "Estimated Parameter"
) +
facet_grid(
param ~ .,
labeller = labeller(
param = as_labeller(c(
"1_1" = "Beta(1,1)",
"a_b" = stringr::str_c("Beta(", lst.beta$a, ",", lst.beta$b, ")")
))
)
)
横軸に試行回数、縦軸にパラメータ p の推定値を表示する。
水平に伸びた直線はパラメータ p の真の値 0.3 を示している。
上下で事前分布が異なる事に注意。
- $Beta(1,1)$/$Beta(3,6)$ ともに試行回数が少ない範囲では推定量ごとの挙動に差異が見られる
- 試行回数が大きくなると推定量による差異はほぼ見られくなる
- EAP(赤色) > MAP(青色) の傾向がある(3.2.1 で後述)
3.2.1 EAP > MAP について
特定の状況においてほぼ EAP > MAP が成立する事を示す。
以下では EAP と MAP の差分を考える事で上記を検証していく。
\begin{eqnarray} \hat{\theta}_{EAP} - \hat{\theta}_{MAP} = \frac{ a + \sum x_{j} }{ n + a + b } - \frac{a + \sum x_{j} - 1}{n + a + b - 2}. \nonumber \end{eqnarray} 上記は分母が基本的に正となるので、計算を楽にするため以下では分子だけを考える。 \begin{eqnarray} 分子 &=& \{ (a + \sum x_{j})(n + a + b - 2) - (a + \sum x_{j} - 1)(n + a + b) \} \nonumber \\ &=& \Bigl[ \bigl\{ (a + \sum x_{j} - 1)(n + a + b - 2) + (n + a + b - 2) \bigr\} - (a + \sum x_{j} - 1)(n + a + b) \Bigr] \nonumber \\ &=& \{ (a + \sum x_{j} - 1)(- 2) + (n + a + b - 2) \} \nonumber \\ &=& \{ (b - a) + 2n (\frac{1}{2} - \frac{1}{n} \sum x_{j}) \} \nonumber \end{eqnarray} 上記より、パラメータ $p$ の不偏推定量である標本平均 $\frac{1}{n} \sum x_{j}$ が $\frac{1}{n} \sum x_{j} < \frac{1}{2}$ を満たせばほぼ $\hat{\theta}_{EAP}>\hat{\theta}_{MAP}$ が成立する。
今回はベルヌーイ分布の真のパラメータが $p = 0.3$ であり $\frac{1}{2}$ より小さい事からほぼ \begin{eqnarray} \therefore \hat{\theta}_{EAP} > \hat{\theta}_{MAP} \nonumber \end{eqnarray} が成立するものと考えられる(適当)。
3.3 試行回数による分布の変化
試行回数の増加に伴う分布の変化をマクロな視点で確認する。
df.estimations %>%
dplyr::select(n, post_dists) %>%
# 事後分布の抽出
tidyr::unnest(post_dists) %>%
# => long-form
tidyr::pivot_longer(cols = c(post_d_1_1, post_d_a_b), names_to = "param", values_to = "density") %>%
# 可視化
ggplot(aes(n, p)) +
geom_tile(aes(fill = density), show.legend = F) +
scale_fill_gradient(low = "#132B43", high = "tomato") +
labs(
x = "Trials",
y = "p"
) +
facet_grid(
param ~ .,
labeller = labeller(
param = as_labeller(c(
"post_d_1_1" = "Beta(1,1)",
"post_d_a_b" = stringr::str_c("Beta(", lst.beta$a, ",", lst.beta$b, ")")
))
)
) +
# 不要な余白を除去
coord_cartesian(expand = F)
横軸に試行回数、縦軸にパラメータ p を表示し、各点における事後分布の確率密度を色で表現する。
黒に近いほど確率密度が低く、赤く明るいほど確率密度が高い事を示す。
上下で事前分布が異なる事に注意。
- 全体を外観すると事前分布が異なる事による差異はほぼ見られない
- 左端の方では明確な赤色が見られず全体としてぼやけた感じとなっている
- 右側に進むにつれて赤と黒が明確に分離していく様子が見て取れる
- 試行回数の増加と共にパラメータ推定の確信度が上がっていると考えられる
- 試行回数が大きくなると分布に殆ど変化が見られなくなり、多少のデータ傾向の揺れに振り回されなくなってくる(左端の挙動と対称的)
上記から、ある程度の試行回数が存在しない限りパラメータ p の推定はあまり意味を持たない可能性があると思われる。
まとめ
- サンプルが少ない場合に、MLE はデータに過度に反応し、データによってはかなり極端な値を提示してしまう
- サンプルが少ない場合に、推定された事後分布はデータに過度に反応する可能性がある
- サンプルが少ない場合に、推定された事後分布は事前分布の違いに大きく影響を受ける可能性がある
- サンプルが少ない場合に、点推定量(MLE/MAP/EAP)による違いが現れる可能性がある
- サンプルが増加するにつれ、推定される事後分布が多少のデータ傾向の揺れに影響を受けづらくなり安定する
- サンプルが増加するにつれ、推定される事後分布は事前分布の違いにあまり影響を受けなくなる
- サンプルが増加するにつれ、点推定量の違いによる差異はほぼ見られなくなる
- ある程度のサンプルが存在しないとパラメータの推定はかなり厳しい